
I recall the days of my youth when “good” math instruction happened in quiet classrooms with students sitting in desks arranged in rows while working problems from their textbook. In recent visits to mathematics classrooms in our region, students were working together, engaging in discourse, creating visual models and questioning one another’s strategies to solve problems in context. There was an intentional focus on student conversations around the development of mathematical ideas. There was also time to allowstudents to revise their thinking and try another approach to solving the math task at hand. I had a strong sense that students were “owning” the mathematics they were engaged in, including their successes and their mistakes.
I would like to share with you an experience I had visiting a school in our region; I was amazed at the mathematical understanding that was evidenced in the conversation 7th graders were having in class…
The students were working on the following task:
|
Noah drewanequilateral triangle with sides 5 inches in length. He wanted to increase the length of each side by inches so that the triangle was still equilateral and had a perimeter of 20 inches.
|
 |
Students read the prompt the first time and were asked to think about what they noticed and what they wondered. Next students shared their noticing and wondering with a partner and then with the whole class. Their teacher recorded the results.
Noticings:
- The triangle is an equilateral
- Each side length measures 5 inches
- The side lengths add up to 15 inches
- Noah wants to increase the perimeter by 5 inches on each side
Wonderings:
- What is an "equilateral" triangle?
- By how much do we need to increase the side length?
- What is the "perimeter"?
- How do you know what to add to each side?
- What does 5 divided by 3 = ?
Students read the prompt a second time and decided, individually, what approach they would take to begin to solve the problem. After a few minutes, students shared their thinking with a new partner. Each student was encouraged to follow the prompt:
I want to show the increase in side length by _____.
Several different approaches surfaced. Each pair of students shared what they thought with another pair. The teacher provided sentences frames for students to either agree, disagree, or provide comments or thoughts on their partner’s approach. Students then went back to work on the problem with this additional shared learning.These were a few of the student samples that the teacher selected to be shared with the whole class.
Some examples of their thinking and discussionsare shown below:
Example 1:
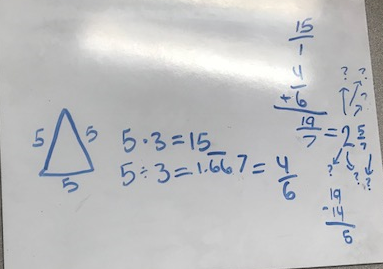 |
 |
|
| Example 2: | ||
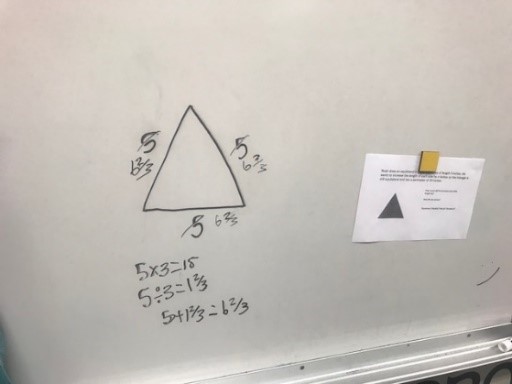 |
 |
|
| Example 3: | ||
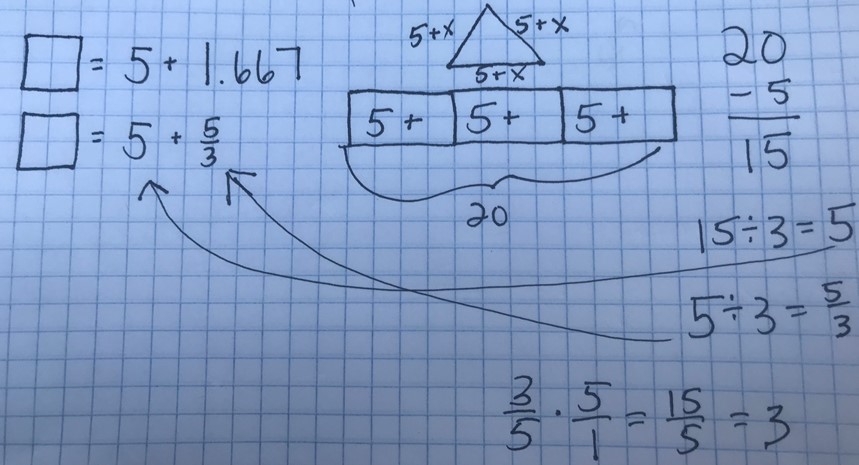 |
||
|
Teacher: Can you explain your thinking? |
 |
Students continued their discussion for a few more minutes. The teacher left them with the question:How does the first model connect to the triangle and tape diagrams?
The students had some private think time and then were asked to write down their comments as a type of exit reflection.
I left the classroom with student work samples to ponder. So much discussion during the class time had revealed student thinking about a lot of big mathematical ideas. The teacher had a picture, although not complete, yet, of what her students understood about fractions, division, ratios, tape diagrams and mathematical expressions-which was her content for the next lesson. What I had witnessed was radically different from the math education I had received!
Currently, mathematics is described as a social endeavor. Sherry Parish, Kathy Richardson, Ruth Parker, Cathy Humphreys, Jo Boaler, Dan Meyer and Graham Fletcher are a few of the mathematics leaders who have contributed to increased student discourse in math classrooms around meaningful and engaging problems. Mathematics materials and tasks now provide prompts and samples for teacher-student and student-student conversations in order to give teachers an example of what mathematical discourse could look like. Math is no longer seen as an individual activity; instead, mathematical knowledge and understanding are built through discourse and the sharing of mathematical approaches and understanding collectively by both the teachers and the students. Math classrooms are becoming a place where students are becoming mathematical thinkers.



